Adjacent heptagons on hyperbolic plane
All elements returned by adjacent function from the previous post indeed correspond to the tiles adjacent to
the given one. And they indeed are arranged in counter-clockwise order.
So what’s the problem?
adjacent :: Heptagon -> [Heptagon]
adjacent (Heptagon h) = map Heptagon (
let
grandparent = up (up h)
left_cousin = left h
right_cousin = right h
grandchildren = [h2 | h1 <- down h,
h2 <- down h1]
in
[grandparent] ++
[left_cousin] ++
grandchildren ++
[right_cousin]
)Depending whether it’s $0$ or $1$, tile has three or two grandchildren (in other words, sector subdivides into three or two subsectors). It means this function returns six or five elements. One or two adjacent tiles are missing.
Every generation (white or yellow strip in the picture) is kind of like Fibonacci word, but infinite in both directions.
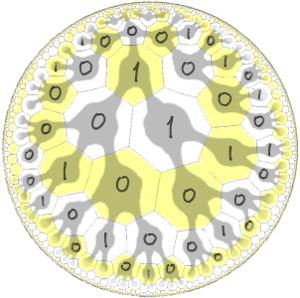
Subwords $11$ and $000$ never occur in a Fibonacci word. It leaves only four possible trigrams: $010$, $001$, $100$, and $101$.
I’ll state without proof that which particular tiles are missing in the output
of the original adjacent function is determined entirely by the types of
its input tile and its immediate left and right “cousins”.
Here are these four cases:

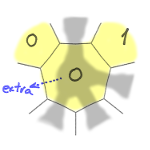
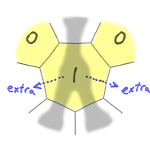
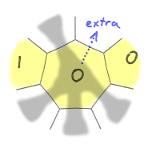
With these extra tiles accounted for,
function adjacent takes the following form:
adjacent :: Heptagon -> [Heptagon]
adjacent (Heptagon h) = map Heptagon (
let
grandparent = up (up h)
left_cousin = left h
right_cousin = right h
grandchildren = [h2 | h1 <- down h,
h2 <- down h1]
in
[grandparent] ++
(if not (isMature left_cousin) &&
not (isMature right_cousin)
then [left grandparent] -- 101
else []) ++
[left_cousin] ++
(if isMature left_cousin
then [left (head grandchildren)] -- 010, 001
else []) ++
grandchildren ++
(if isMature left_cousin &&
isMature right_cousin
then [right (last grandchildren)] -- 010
else []) ++
[right_cousin] ++
(if not (isMature left_cousin) &&
isMature right_cousin
then [right grandparent] -- 100
else [])
)Now implementation of heptagrid coordinate system is complete.
Related stuff
HyperRogue has source code available, and its relevant part, heptagon.cpp, is surprisingly concise. However, it is not strictly speaking a coordinate system as I informally define it, more like some mutable interconnected graph of tiles that is constructed as we walk the grid, patching the pointers along the way. One inconvenient consequence is that data structure that has to be kept in memory depends not only on the tiles we want to represent at the moment, but on the tiles that were visited before. Probably not a big deal in practice. Also, pointers to existing adjacent tiles simplify computing adjacent tiles for newly created tiles – something that requires handling of multiple cases in pure functional approach.
Maybe I just don’t know the right keywords, but it appears there is a single
person on the whole Internet who writes about computational aspects of
hyperbolic tilings, Maurice Margenstern. What I described in this series
of posts mostly mirrors his technique from the book
“Small Universal Cellular Automata in Hyperbolic Spaces: A Collection of Jewels”
(although it took me some reinventing the wheel to fully appreciate that).
Key idea there is spanning the sector of the grid with 2,3-Fibonacci tree.
I use rule $\{0 \to 010, 1 \to 01\}$ instead of prof. Margenstern’s rule
$\{0 \to 100, 1 \to 10\}$, to stress the connection with
rabbit rule
$\{0 \to 01, 1 \to 0\}$. This allows me to bypass Fibonacci number notation
and deal with 2,1-Fibonacci tree directly. Not sure it’s a win, though:
on one hand, it makes things more tangible in my eyes, on the other,
I have to decide between four cases for extra adjacent tiles,
while Margenstern’s rules only distinguish three (actually, I suspect that
in the correctness proof there still will be four cases, but I haven’t checked).
What I’m pretty sure is an improvement, is using a tree that grows at the root. Both Margenstern and Zeno Rogue cover hyperplane with seven sectors surrounding a central tile, which requires special effort to stitch these petals together. In my system there is a single uniform tree that extends infinitely in all directions. Fewer special cases, less room for errors.